Graph Colouring Generator

Given an undirected graph with vertex set \(V\) and edge set \(E\) and a a set of \(n\) colours, Graph Colouring consists in finding whether we can colour every node of the graph in one of these \(n\) colours such that no edge connects nodes of the same colour. We therefore need \(nN\) spins to anneal the problem, where \(N\) is the number of vertices of the graph. The classical complexity of the best known approximate algorithm for this problem is \(O(N(\log \log N)^2 (\log N)^3)\).

The GraphColouringGenerator can be used to generate batches to solve the Graph Colouring problem on an input graph. Some examples using different types of job generation and QPUs on some simple graphs are shown below:

QAOA job generation

import networkx as nx
import numpy as np
from qat.generators import GraphColouringGenerator
from qat.plugins import ScipyMinimizePlugin
from qat.qpus import get_default_qpu

graph = nx.Graph()
graph.add_nodes_from(np.arange(4))
graph.add_edges_from([(0, 1), (0, 2), (1, 2), (1, 3), (2, 3)])

scipy_args = dict(method="COBYLA", tol=1e-5, options={"maxiter": 200})
graph_colouring_application = GraphColouringGenerator(job_type="qaoa") | (ScipyMinimizePlugin(**scipy_args) | get_default_qpu())
combinatorial_result = graph_colouring_application.execute(graph, 3)

print(combinatorial_result.subsets)

[[2], [1], [0, 3]]

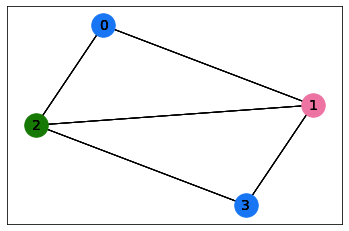
The parsed combinatorial result can also be displayed with NetworkX using the display() method:

combinatorial_result.display()

../../images/graph_colouring_generator_result.png

SQA job generation

import networkx as nx
import numpy as np
from qat.generators import GraphColouringGenerator
from qat.qpus import SimulatedAnnealing
from qat.core import Variable
from qat.opt.sqa_best_parameters import sqa_best_parameters_dicts

graph = nx.Graph()
graph.add_nodes_from(np.arange(4))
graph.add_edges_from([(0, 1), (0, 2), (1, 2), (1, 3), (2, 3)])

# Create a temperature function
t = Variable("t", float)
temp_max = sqa_best_parameters_dicts["GraphColouring"]["temp_max"]
temp_min = sqa_best_parameters_dicts["GraphColouring"]["temp_min"]
temp_t = temp_min * t + temp_max * (1 - t)  # annealing requires going from a high to a very low temperature
n_steps = 5000

graph_colouring_application = GraphColouringGenerator(job_type="sqa") | SimulatedAnnealing(temp_t, n_steps)
combinatorial_result = graph_colouring_application.execute(graph, 3)

Similarly, the method display() can be used to display the result:

combinatorial_result.display()

AQO job generation

import networkx as nx
import numpy as np
from qat.generators import GraphColouringGenerator

graph = nx.Graph()
graph.add_nodes_from(np.arange(4))
graph.add_edges_from([(0, 1), (0, 2), (1, 2), (1, 3), (2, 3)])

graph_colouring_generator = GraphColouringGenerator(job_type="aqo")
aqo_batch = graph_colouring_generator.generate(None, graph, 3)

Currently, the analog qpus that can be used to execute the underlying Schedule are only available on Qaptiva. Therefore, the generated aqo_batch here can be passed to Qaptiva for execution.