Crossing lattice

The crossing lattice is an embedding technique used to solve combinatorial problems on Rydberg atom devices. There is a wide range of optimization problems which can be mapped on Rydberg atom devices using the crossing lattice. This section focuses on the Maximum Weighted Independent Set (MWIS) and Quadratic Unconstrained Binary Optimization (QUBO).

Maximum Weighted Independent Set (MWIS)

Given a graph \(G\) with a vertex set \(V\), an edge set \(E\) and weight map \(f\), the problem consists on finding the weightiest Independent set of the graph.

The idea of the crossing lattice is to use ancillary nodes to map the graph on a triangular lattice. The latter can be seen as an extension of the triangular upper part of the adjacency matrix of the input graph.

If we take the sample graph:

import networkx as nx
graph = nx.Graph()
graph.add_nodes_from([1, 2, 3, 4, 5])
graph.add_edges_from([(1, 2), (1, 4), (1,  5), (3, 2), (3, 4), (3, 5)])

nx.draw(graph, with_labels=True)

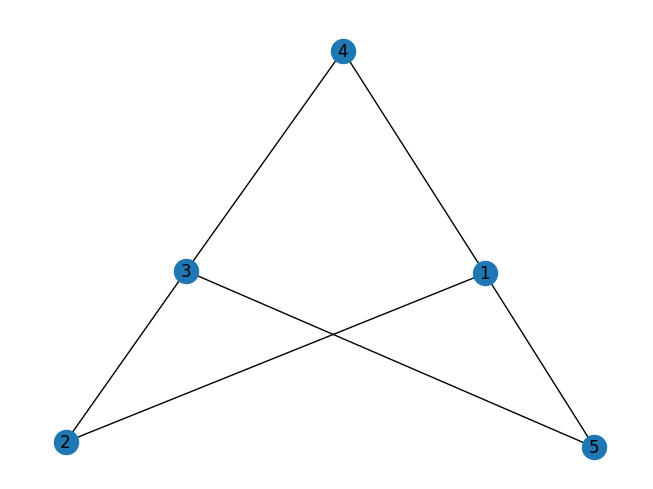
A higher level representation of the crossing lattice embedding of the graph below is the following:

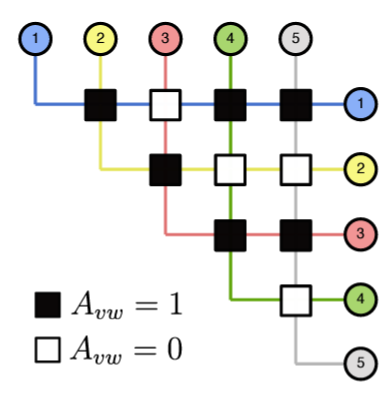
Each part of this diagram (lines, white boxes, black boxes) are group of nodes (connected in a specific way) denoted gadgets. With such an embedding of the graph, we keep the connectivity of the initial graph. By choosing the weights of the crossing lattice graph in a specific way, we can show that the MWIS of the crossing lattice graph corresponds to that of the initial graphs.

To use the crossing lattice embedding for MWIS/MIS problems one can use the methods to_job() or ryd_job() of MWIS

from qat.opt import MWIS

pbm = MWIS(graph)
job = pbm.to_job("ryd")

After executing this job, the result can be decoded using decode_rydberg().

Quadratic Unconstrained Binary Optimization (QUBO)

Quadratic Unconstrained Binary Optimization (QUBO) consists in, given a real symmetric matrix \(Q\), minimizing the following cost function:

\[H = -x^TQx = -\sum_{i, j} J_{ij}s_i s_j - \sum_i h_i s_i\]

Please refer to our page describing the QUBO formalism for more information on this equality. We can encode such a problem by exploiting the structure of the crossing lattice:

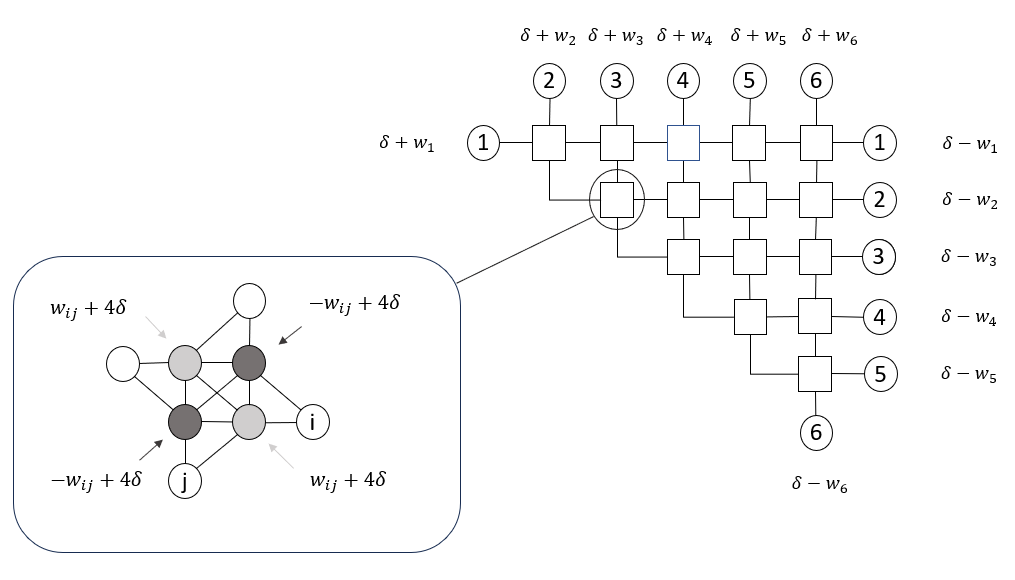
Here, \(w_{ij} = J_{ij}\) and \(w_i = h_i\). With such an encoding we can prove that the Maximum Weighted Independent Set of the corresponding graph corresponds to the mimimum of \(H\)

import numpy as np
from qat.opt import QUBO

# QUBO matrix
matrix = np.array([
   [ 1., -2., 2],
   [-2., -1, 0],
   [2, 0, 1]
])

pbm = QUBO(matrix)
job = pbm.to_job("ryd")

After executing this job, the result can be decoded using decode_rydberg().