Max Cut Generator
Given an undirected graph with vertex set \(V\) and edge set \(E\), the problem consists in partitioning the graph into two subgraphs connected by the maximum number of edges. Annealing the problem needs \(\#V\) spins (one spin per vertex of the graph).
The MaxCutGenerator can be used to generate batches to solve the Max Cut problem on an input graph.
Some examples using different types of job generation and QPUs on some simple graphs are shown below:
import networkx as nx
from qat.generators import MaxCutGenerator
from qat.plugins import ScipyMinimizePlugin
from qat.qpus import get_default_qpu
graph = nx.full_rary_tree(3, 6)
scipy_args = dict(method="COBYLA", tol=1e-5, options={"maxiter": 200})
max_cut_application = MaxCutGenerator(job_type="qaoa") | (ScipyMinimizePlugin(**scipy_args) | get_default_qpu())
combinatorial_result = max_cut_application.execute(graph)
print("The nodes in the first subgraph are", combinatorial_result.subsets[0])
print("The nodes in the second subgraph are", combinatorial_result.subsets[1])
# The cost here is negative since all combinatorial optimization problems are defined as a minimization problem, so a factor of -1 is needed
print("The number of edges that are cut is", -1 * combinatorial_result.cost)
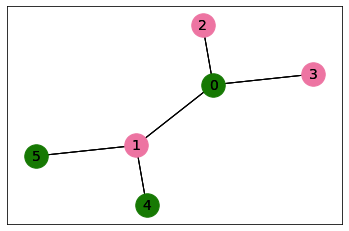
The nodes in the first subgraph are [0, 4, 5]
The nodes in the second subgraph are [1, 2, 3]
The number of edges that are cut is 5.0
The parsed combinatorial result can also be displayed with NetworkX using the
display() method:
combinatorial_result.display()
import networkx as nx
from qat.generators import MaxCutGenerator
from qat.qpus import SimulatedAnnealing
from qat.core import Variable
from qat.opt.sqa_best_parameters import sqa_best_parameters_dicts
graph = nx.full_rary_tree(2, 30)
# Create a temperature function
t = Variable("t", float)
temp_max = sqa_best_parameters_dicts["MaxCut"]["temp_max"]
temp_min = sqa_best_parameters_dicts["MaxCut"]["temp_min"]
temp_t = temp_min * t + temp_max * (1 - t) # annealing requires going from a high to a very low temperature
n_steps = 5000
max_cut_application = MaxCutGenerator(job_type="annealing") | SimulatedAnnealing(temp_t, n_steps)
combinatorial_result = max_cut_application.execute(graph)
print("The nodes in the first subgraph are", combinatorial_result.subsets[0])
print("The nodes in the second subgraph are", combinatorial_result.subsets[1])
# The cost here is negative since all combinatorial optimization problems are defined as a minimization problem, so a factor of -1 is needed
print("The number of edges that are cut is", -1 * combinatorial_result.cost)
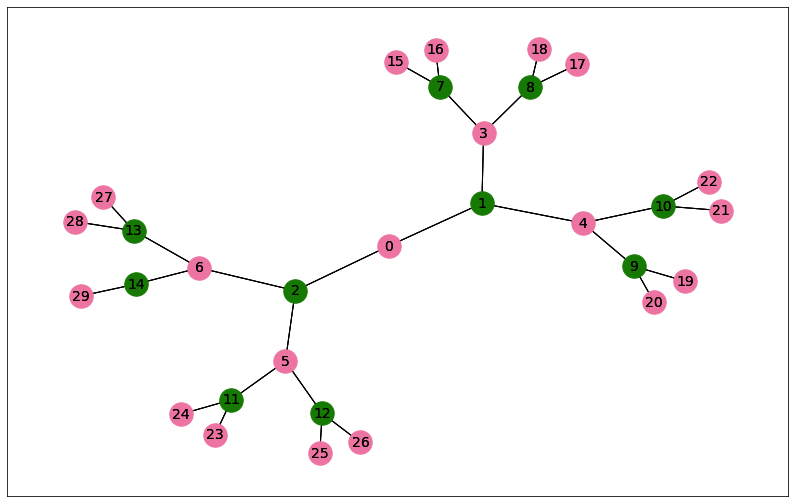
The nodes in the first subgraph are [1, 2, 7, 8, 9, 10, 11, 12, 13, 14]
The nodes in the second subgraph are [0, 3, 4, 5, 6, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29]
The number of edges that are cut is 29.0
Similarly, the method display() can be used
to display the result:
combinatorial_result.display()
import networkx as nx
from qat.generators import MaxCutGenerator
graph = nx.full_rary_tree(3, 6)
max_cut_generator = MaxCutGenerator(job_type="schedule")
schedule_batch = max_cut_generator.generate(None, graph)
Currently the analog qpus that can be used to execute the schedule are only available on Qaptiva. Therefore the generated schedule_batch here can be passed to Qaptiva for execution.