qat.lang
This module provides a powerful API to create quantum circuits. Quantum circuits can be composed of quantum gates (including user defined gates), intermediate measurements, classically controlled gates, etc.
Programming tools
This module provide tools to create advanced quantum circuit. Designed quantum circuit is detailed in the user guide, section gate-based programming
Program class, to create quantum circuit |
|
qfunc decorator, to define a gate-based quantum function |
|
qrout decorator, to define a circuit using a function |
Default gate set
myQLM provides a set of predefined gates, which can be used to create quantum circuits.
Definition of the Toffoli gate |
|
Definition of the Controlled NOT gate |
|
Definition of the Controlled Z gate |
|
Definition of the H gate |
|
Definition of the I gate |
|
Definition of the iSWAP gate |
|
Definition of the Phase shift gate |
|
Definition of the RX gate |
|
Definition of the RY gate |
|
Definition of the RZ gate |
|
Definition of the S gate |
|
Definition of the \(\sqrt{SWAP}\) gate |
|
Definition of the SWAP gate |
|
Definition of the T gate |
|
Definition of the X gate |
|
Definition of the Y gate |
|
Definition of the Z gate |
Additionally, myQLM provides somes gates which can be used to directly build a Program.
RZ gate similar to the one in default gate set |
|
R gate from AQT gate set (also known as PRX) |
|
RXX gate from AQT gate set |
CZ gate similar to the one in default gate set |
|
I gate similar to the one in default gate set |
|
RX gate similar to the one in default gate set |
|
RZ gate similar to the one in default gate set |
|
X gate similar to the one in default gate set |
|
ECR gate from IBM gate set |
|
RZZ gate from IBM gate set |
|
\(\sqrt{X}\) gate from IBM gate set |
|
ZZ gate from IBM gate set |
GPi2 gate (Gate Pi/2) from IonQ gate set |
|
GPi gate (Gate Pi) from IonQ gate set |
|
PMS (Phased Mølmer-Sørensen gate) gate from IonQ gate set |
|
ZZ gate from IonQ gate set |
CZ gate similar to the one in default gate set |
|
RZ gate similar to the one in default gate set |
|
PRX gate from IQM gate set |
RZ gate similar to the one in default gate set |
|
K gate from Quobly gate set |
|
ZZ gate from Quobly gate set |
Gate structures
All classes describing unitary operators inherit from the Gate class.
User defined gate |
|
Decorator creating a quantum gate |
|
Subcircuit behaving as a gate object |
|
Parent class for all quantum gates / unitary operators |
|
Parametrized gate |
Quantum types
Quantum boolean and expressions
Quantum bool |
|
Array of quantum bool |
|
Quantul clause |
Quantum integers
Arithmetic expression |
|
Comparison expression |
|
Quantum integer |
Managing registers
Clasical formula |
|
Classical bit class |
|
Register of cbits |
|
Quantum bit class |
|
Register of qubits |
Gate set management
Gate set generator |
External gate sets
myQLM provides some gate set builder, corresponding to the gate set of known QPUs:
Generate a gate set corresponding to AQT’s hardware |
|
Generate a gate set corresponding to IBM’s hardware |
|
Generate a gate set corresponding to IonQ’s hardware |
|
Generate a gate set corresponding to IQM’s hardware |
|
Generate a gate set corresponding to Quobly’s hardware |
Linker and low level circuit manipulation
In pyAQASM, gates can be specified using various representations. They can be purely abstract (a name and a set of parameter values, such as RZ, [PI/2]). To this abstract syntax, one can attach a matrix, or even a subcircuit that implements this gate (this is the case of adders of the arithmetic library for instance).
Circuits are generated in two steps:
first a skeleton of the circuit is generated (for instance adders will be gates called ADD in this skeleton)
then a subcircuit is generated and attached to this abtract gate.
This second step is handled by a class called Linker. It can be useful in some settings to manipulate this Linker object in order to replace
gates by subcircuits, or to generate matrices in order to simulate the circuit.
pyAQASM linker |
Quantum labraries and basic algorithms
This module provides a set of routine to simplify the implementation of quantum circuits
Arithmetic routines
pyAQASM comes with a pre-implemented set of arithmetic routines. Since there are different approaches to implement arithmetic routines, we provide various implementation of some low-level routines such as additions and additions by a classical constant. Higher level routines are then implemented by calling some implementation of these lower level routines.
The following diagram sums up the various routines and their implementation. Arrows mean “uses”, green boxes indicates the implementation strategy:
QFT means QFT-based arithmetic
CARRY means ripple-carry based arithmetic
INDEP means agnostic. These routines call lower level routines, indepentently from their implementation.
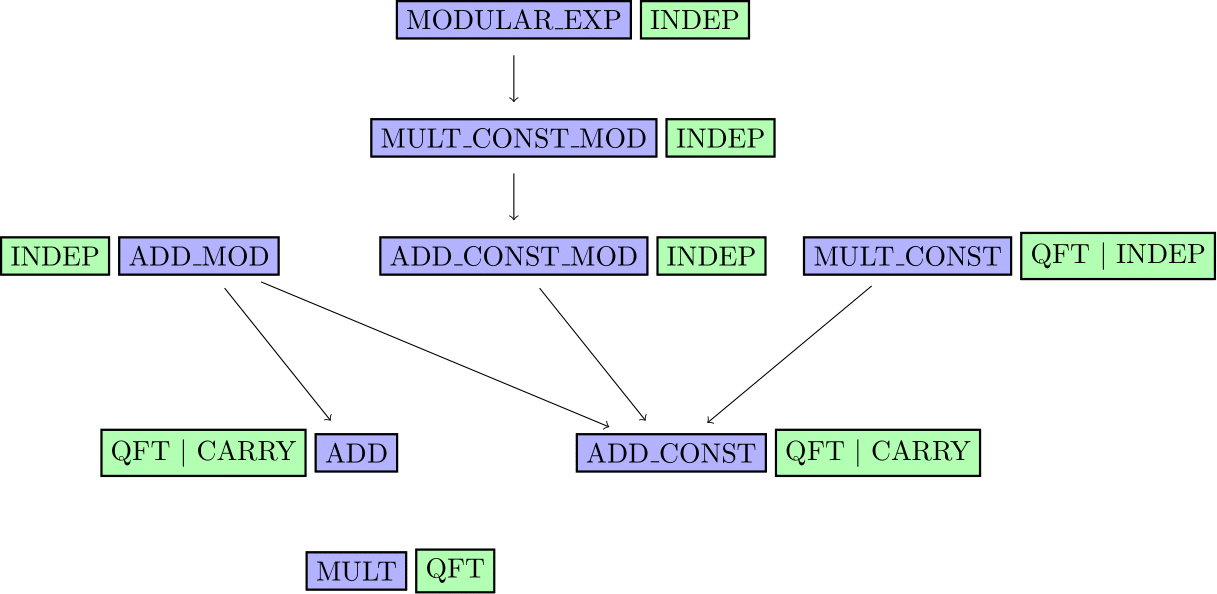
The routines are separated into three distinct namespaces according to these three types of implementation strategy: QFT, CARRY, INDEP.
Warning
All methods are decorated using @build_gate which turn them into AbstractGates. To access the underlying routine instead of the wrapping gates, the method name can be prefixed with ‘~’.
# will generate a call to an AbstractGate having the QFT as circuit
# implementation
QFT(3)
# will generate a QRoutine object
(~QFT)(3)
The two behaviors are comparable, except that using the U notation allows to skip the inlining step when extracting the circuit (.to_circ method with inline=False) and to link another implementation of gate U later on. Using (~U) will effectively inline the gate no matter what
State preparatation and QRAM
A class representing a Kerinidis-Prakash tree for a QRAM |
Algorithms
There are a few basic algorithms present in the qat.lang.algorithms module:
Single amplification step of Grover’s algorithm |
|
Phase estimation routine |
|
Performs a quantum counting on some oracle |
Additionally, the submodule qat.lang.algorithms.amplification contains some functions that might be useful:
Grover diffusion |
|
Performs a Householder for any unitary |
|
Prepare a uniform distribution from state \(|0...0\rangle\) |